静电场高斯定理

约 5321 个字 14 张图片预计阅读时间 18 分钟

基本实验定律 ¶

1747 年，富兰克林提出了电荷的概念
1897 年，汤姆孙证明阴极射线是一种粒子流，其具有确定的荷质比，称其为电子。
1911 年，卢瑟福进行了 $\alpha$ 粒子轰击金箔的散射实验，发现了原子核。

电荷是量子化的。

电荷守恒定律：在一孤立系统内发生的任何过程中总电荷数不变，即在任一时刻存在于系统中的正电荷与负电荷的代数和不变。

电荷相对论不变性：物体所带的电量与物体的运动状态无关。即在不同的参考系观察同一个带电粒子，电荷量不变。

库仑定律：

\[ \overrightarrow F=\frac{1}{4\pi\varepsilon_0}\frac{q_1q_2}{r^3}\,\overrightarrow r \]

式中， $\varepsilon_0$ 是自然界的一个基本常量，称为真空介电常量。单位为 $\mathrm{C^2\cdot N^{-1}\cdot m^{-2}}.$

库仑定律在 $10^{-17}m\sim 10^{7}m$ 范围内成立。

电场强度及其叠加原理 ¶

电荷是通过电场来相互作用的。（“超距作用”不对）

\[ \text{电荷}\leftrightharpoons\text{电场}\leftrightharpoons\text{电荷} \]

一般而言，两个有相对运动的电荷 $q$ 与 $q'$ ，它们之间的相互作用力不是一对作用力和反作用力。它们的互相作用也会导致总动量不守恒。因此，场也具有动量，加上场的动量总动量是守恒的。电场也具有能量和质量。

静电场是保守力场。

由于运动是相对的，因此电场和磁场的区别也是相对的。不同惯性系下观察物体可能会激发出不同的电场或磁场。

场强 ¶

空间某一点的电场强度是这样一个矢量，其大小等于单位电荷在该点所受到的电场力的大小，其方向与正电荷在该点所受到的电场力的方向一致。它反应的是电场本身的性质。

\[ \overrightarrow E = \frac{\overrightarrow F}{q_0} \]

在国际单位制中，电场强度的单位是 $\mathrm{N\cdot C^{-1}}$ . 或者 $\mathrm{V \cdot m^{-1}}$ .

场强叠加原理 ¶

点电荷系在某点产生的场强，等于每个点电荷单独存在时，在该点产生的场强的矢量和。这是电场的基本性质之一。

\[ \overrightarrow E=\sum_{i=1}^{n}\overrightarrow E_i \]

对于从电荷分布求场强的问题至此基本解决，剩下的交给高等数学。

下面介绍一些常见的电荷分布和对应场强

常见的电荷分布并求场强 ¶

点电荷 ( 系 ) ¶

没什么好说的，一个点电荷 ( 系 ) 产生的场强有库仑定律直接可以写出来：

\[ \overrightarrow E=\sum_{i=1}^n \frac{1}{4\pi\varepsilon_0}\frac{q_i}{r_i^3}\ {\overrightarrow r_i} \]

电偶极子 ¶

电偶极子是大小相等、符合相反的点电荷 $+q$ 和 $-q$ 组成的系统。两个电荷间距为 $l$ . 矢量 $\overrightarrow p=q\,\overrightarrow l$ 称为电偶极矩，简称电矩，规定方向由负电荷指向正电荷。

电偶极子中垂线上一点的电场强度的矢量式为： $$ \overrightarrow E=-\frac{1}{4\pi\varepsilon_0}\frac{\overrightarrow p}{r^3} $$

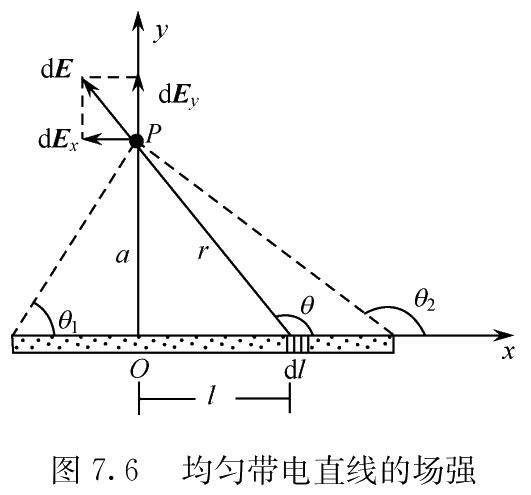
细棒 ¶

长度为 $L$ 的均匀带电直线，线电荷密度为 $\lambda$ ，线外一点 $P$ 到直线的距离为 $a$ ， $P$ 点同直线两端点的连线与直线间夹角分别为 $\theta_1$ 和 $\theta_2$ ， $P$ 点的场强为： $$ E_x=\frac{\lambda}{4\pi\varepsilon_0a}(\sin\theta_2-\sin\theta_1) \ E_y=\frac{\lambda}{4\pi\varepsilon_0a}(\cos\theta_1-\cos\theta_2) $$ 当 $\theta_1=0,\theta_2=\pi$ 时，就有无限长均匀带电直线的场强公式 $$ E_x=0, E_y=\frac{\lambda}{2\pi\varepsilon_0a} $$ 当 $\theta_1=\frac{2}{\pi},\theta_2=\pi$ 时，就有半无限长均匀带电直线的场强公式 $$ E_x=-\frac{\lambda}{4\pi\varepsilon_0a}=-E_y $$ 当 $a\gg l$ 时，由 $$ E\approx \frac{\lambda}{4\pi\varepsilon_0a}(\tan\theta_2-\tan\theta_1)=\frac{\lambda}{4\pi\varepsilon_0a}(\frac{l}{a})=\frac{q}{4\pi\varepsilon_0a^2} $$ 可知，此时细棒产生的场强等价于点电荷产生的场强。

均匀带电细圆环的轴线上 ¶

半径为 $R$ 的均匀带电细圆环，总电量为 $q$ ，求圆环轴线上点 $P$ 的场强。 $$ E=E_{//}=\frac{1}{4\pi\varepsilon_0}\frac{xq}{(x^2+R2)^{\frac{3}{2}}} $$ 在圆环中心 $(x=0)$ 处，场强为零。

当 $x\gg R$ 时， $E=\frac{q}{4\pi\varepsilon_0x^2}$ ，此时可以看作一个点电荷。

均匀带电薄圆盘的轴线上 ¶

半径为 $R$ 的均匀带电薄圆盘，总电量为 $Q$ ，求薄板轴线上点 $P$ 的场强。

\[ E=\frac{\sigma}{2\varepsilon_0}\Big(1-\frac{x}{\sqrt{x^2+R^2}}\Big) \]

其中 $\sigma$ 是薄板的面电荷密度，即 $\sigma=\frac{Q}{\pi R^2}$ .

当 $x \gg R$ 时，有无限大均匀带电平面产生的场强公式：

\[ E=\frac{\sigma}{2\varepsilon_0} \]

高斯定理 ¶

电通量 ¶

\[ \Phi=\iint_S\overrightarrow E \,\cdot\, \mathrm{d}\overrightarrow S \]

其中 $\overrightarrow S$ 指在曲面某一面元的面积，方向为法向量所指方向。

电通量穿出为正，穿入为负。

高斯定理 ¶

真空中的静电场内，通过任意封闭曲面的电通量等于该封闭曲面所包围的电荷电量的代数和的 $\mathbf{1/\varepsilon_0}$ .

\[ \Phi=\int\kern{-8pt}\int \kern{-23mu} \bigcirc\, \overrightarrow E \cdot\mathrm{d}\,\overrightarrow S=\frac{1}{\varepsilon_0}\int_Q\mathrm{d}q \]

利用高斯公式，可以快速求出具有对称性的带电体的场强分布。

Info

由高斯定理可知，通过封闭曲面的电通量只与封闭曲面内的电荷有关，与曲面外的电荷无关。但是，封闭曲面上各点的电场强度却与空间所有的电荷有关。

Abstract

高斯定理对于任何电场、任何封闭曲面都成立，但是要利用高斯定理简化电场求解，却限于具有高度对称性的电场。

场强环路定理电势 ¶

电场力的功 ¶

在点电荷 $q$ 产生的电场中，将试验电荷 $q_0$ 从 $a$ 点移到 $b$ 点，电场力对 $q_0$ 做的功为：

\[ A_{ab}=\int_a^b q_0 \overrightarrow E \,\cdot\,\mathrm{d}\overrightarrow l=\frac{q_0q}{4\pi\varepsilon_0}\int_{r_a}^{r_b}\frac{1}{r^2}\mathrm{d}r \\ \text{得 } A_{ab}=\frac{q_0q}{4\pi\varepsilon_0}\Big(\,\frac{1}{r_a}-\frac{1}{r_b}\,\Big) \]

场强环路定理 ¶

做功与路径无关的力场称为保守力场。在静电场中，场强沿任意闭合路径的环流等于零。也说明静电场是无旋场，电场线不能是闭合曲线。

\[ {\int \kern{-20mu} \bigcirc}_L\, \overrightarrow E \cdot\mathrm{d}\,\overrightarrow l=0 \]

静电场的环路定理（无旋场）与静电场的高斯定理（有源场）各自独立地反映了静电场性质的一个侧面，来源于不同的实验事实：前者来自点电荷静电场力的各向同性，后者来源于这种静电场力的平方反比关系。这两个定理合起来才能完整地描述静电场。场强环路定理只对静电场适用，对一般的电磁场需要做修正。

电势能电势 ¶

电势能 ¶

通常选定无穷远点的电势能为零。把单位正电荷从a点沿任意路径移动到b点时，静电场力所做的功等于单位正电荷在a、b两点的电势能之差。

结合电势，电场力所做的功可表示为

\[ A_{ab}=q_0\int_a^b\overrightarrow E\,\cdot\,\mathrm{d}\overrightarrow l=q_0U_{ab} \]

电势 ¶

默认无限远处为零势点。对于点电荷， $Q>0$ , 则 $U>0$ 。

\[ U_a=\frac{W_a}{q_0}=\int_a^{\text{零势}} \overrightarrow E\,\cdot\,\mathrm{d}\overrightarrow l \]

电势等于单位正电荷置于该点处时具有的电势能，等于把单位正电荷从该点沿任意路径移到 0 势点处时电场力所做的功。单位为 $\mathrm{J\cdot C^{-1}}$，符号为 $\mathrm{V}\text{伏特}$ 。

电偶极子的电势 ¶

\[ U_P=\frac{\overrightarrow p \cdot \overrightarrow r}{4\pi\varepsilon_0r^2} \]

$\overrightarrow p$ 是电偶极矩。这再一次表明电偶极子的电场性质取决于它的电偶极矩 $\overrightarrow p$ .

场强与电势的关系 ¶

\[ \overrightarrow E=-\mathbf{grad}U \]

场强总是沿电势变化最快的空间方向从高电势指向低电势处。

\[ \overrightarrow E=-\frac{\partial U}{\partial x}\hat{i}-\frac{\partial U}{\partial y}\hat{j}-\frac{\partial U}{\partial z}\hat{k} \]

等势面越密的地方，场强越大。

静电场中的导体 ¶

静电平衡状态和条件 ¶

当把导体放在外电场中时，导体内部的自由电子因受到电场力的作用而做宏观的定向运动，引起导体中的电荷重新分布，这种现象称为静电感应。

导体内部及导体表面上的电荷均无宏观定向运动的状态称为导体的静电平衡状态。

导体静电平衡的条件为

\[ E_\text{内}=0,\,\,E_\text{表面}\perp \text{表面} \]

换句话说，导体为等势体，表面为等势面。

导体的电荷分布 ¶

净电荷只分布在导体表面上。
导体表面处的场强处处表面垂直，其大小 $E=\sigma/\varepsilon_0$
孤立导体的电荷面密度与表面曲率有关，即曲率半径越小，曲率越大，面电荷密度越大。

\[ \frac{\sigma_1}{\sigma_2}=\frac{r_2}{r_1} \]

静电场中的电介质 ¶

电介质的极化束缚电荷 ¶

无论是对于本身分子结构导致分子电荷分布的不对称（极性分子），还是非极性分子在外加电场的作用下发生感应电矩而导致的电荷分布不对称，它们的宏观表现是一样的。在均匀电介质内部的区域仍然是电中性，但表面出现了一定的电荷分布。在外电场的作用下，电介质显示电性的现象，称为电介质的极化。电介质表面出现的电荷称为极化电荷，这些极化电荷不能用传导的方法引走，因而也称为束缚电荷。

电介质的极化程度可以引入电极化强度来描写。

电极化强度 ¶

定义：是单位体积内分子电偶极矩的矢量和。

\[ \overrightarrow P=\frac{\sum\overrightarrow p_i}{\Delta V} \]

其中 $p_i$ 指某一个分子的电矩。 $\Delta V$ 指电介质中的某一小体积。

电极化强度的单位是 $\mathrm{C \cdot m^{-2}}$ . 其量纲与电荷面密度的量纲相同。

实验表明，当电介质中的电场强度不太强时，对各向同性的电介质，其电极化强度与场强成正比，即

\[ \overrightarrow P=\varepsilon_0\chi_e\overrightarrow E \]

式中 $\chi_e$ 为电介质的电极化率。它的量纲为 $\mathrm{1}$ .

电位移电介质中静电场的高斯定理 ¶

金属导体上带的电荷，为了与电介质上的束缚电荷相区别，常称之为自由电荷 $q_0$ , 其电场为 $\overrightarrow E_0$ , 对应的束缚电荷表示为 $q'$ , 其电场为 $\overrightarrow E'$ .

此时总场强为

\[ \overrightarrow E=\overrightarrow E_0+\overrightarrow E' \]

电位移矢量 ¶

在有电介质存在的情况下，引入电位移矢量 $\overrightarrow D$ ：

\[ \overrightarrow D=\varepsilon_0 \overrightarrow E+\overrightarrow P \]

则由高斯定理可以整理出：

\[ \int\kern{-8pt}\int \kern{-23mu} \bigcirc\, \overrightarrow D \cdot\mathrm{d}\,\overrightarrow S=\sum\limits_{in}q_0 \]

电位移矢量的单位为 $\mathrm{C \cdot m^{-2}}$ .

Note

需要强调，虽然电位移的通量仅与闭合曲面内的自由电荷有关，但是电位移矢量不仅仅由空间的自由电荷分布决定，还与束缚电荷有关。

对各向同性的介质，在电场强度不太强的情况下，将 $\overrightarrow P$ 用电极化率替换，则有

\[ \overrightarrow D=\varepsilon_0 \overrightarrow E+\varepsilon_0\chi_e\overrightarrow E=\varepsilon_0(1+\chi_e)\overrightarrow E \]

令 $\varepsilon_r=1+\chi_e$ ，则有

\[ \overrightarrow D=\varepsilon_0\varepsilon_r\overrightarrow E \]

再令 $\varepsilon=\varepsilon_0\varepsilon_r$ , 最终有

\[ \overrightarrow D=\varepsilon\overrightarrow E \]

其中， $\varepsilon_r$ 称为电介质的相对介电常量， $\varepsilon$ 称为电介质的介电常量。

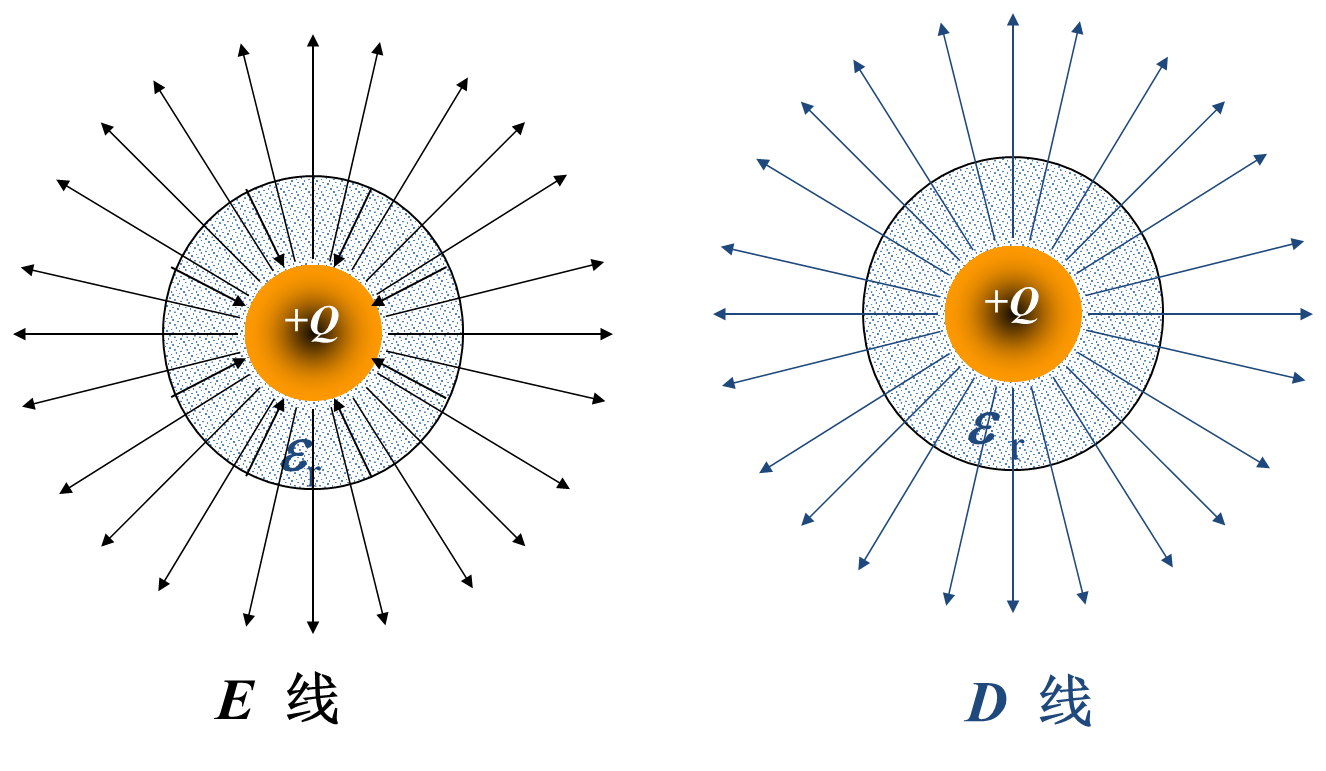
对应于电场强度的具象：电力线，电位移矢量对应的是电位移线。电位移线起于正自由电荷，止于负自由电荷。

电容电容器 ¶

电容 ¶

不同形状和大小的导体达到相同的电势时，其所带电量一般不同。因此，可把导体当作电量的容器，并引人导体的电容这一物理量来描述导体的这种属性。孤立导体的电容 $C$ 定义为

\[ C=\frac{Q}{U} \]

电容的单位是法拉 $\mathrm{F}$ .

真空中的孤立导体球的电容为

\[ C=4\pi \varepsilon_0 R \]

电容器 ¶

通常用两个由电介质隔开的、彼此靠得很近的导体薄板、导体薄球面或薄柱面组成电容器。这两块导体称为电容器的极板。电容器的电容定义为

\[ C=\frac{Q}{U_1-U_2} \]

实验和理论都表明，它的值只取决于极板的大小、形状、相对位置及其间所充的电介质等因素。对给定的电容器与极板是否带电无关。

下面是几种典型电容器电容的计算 .

平板电容器 ¶

$S$ 是极板相对着的面积 , $d$ 为板间的距离，相对介电常量为 $\varepsilon_r$ 的电介质充满极板之间 . 忽略边缘效应 .

\[ \left\{ \begin{matrix} C=\frac{Q}{U}\hfill \\ E=\frac{\sigma}{\varepsilon}=\frac{Q}{\varepsilon S}\hfill \\ U=Ed \hfill \end{matrix} \right. \]

得到

\[ C=\frac{\varepsilon S}{d} \]

板间所充满的电介质使得电容增大到板间真空时的电容的 $\varepsilon_r$ 倍 .

如果题目更换了板夹的电介质，则只能积分求得，或者依据电容器串并联方法速求。

圆柱电容器 ¶

由于圆柱电容器中间的电介质可以改变为夹层或间隔排放的形式，不能只记公式，故掌握方法最重要。

由电位移通量的高斯定理算出场强的表达式；
再积分出两筒间的电势差；
依据定义即可求出电容表达式。

下面是两筒之间充满介电常量为 $\varepsilon$ 的电介质情况下的电容表达式

\[ C=\frac{2\pi \varepsilon L}{\ln(\frac{R_2}{R_1})} \]

球形电容器 ¶

球形电容器由两个同心的导体球壳构成。如果两球壳间充满电介质，介电常量为 $\varepsilon$ ，用与上面类似的方法就可求出球形电容器的电容为

\[ C=\frac{4\pi\varepsilon R_1R_2}{R_2-R_1} \]

可以发现，当 $R_2\to\infty$ 时，表达式变成了真空中孤立导体球的电容表达式。

串联与并联 ¶

串联：

\[ \frac{1}{C_\text{总}}=\sum_{i=1}^{n}\frac{1}{C_i} \]

串联电容器组的特点是：等效电容小于组内任意一个电容器的电容；等效电容两端的电压为组内各电容器端电压之和，即串联提高了耐压性。

并联：

\[ C_\text{总}=\sum_{i=1}^{n}C_i \]

并联电容器增大了电容，但耐压性并未提高，只要其中一个电容器被击穿，整个电容器组就意味着被击穿了。

利用串并联巧解电容 ¶

例题 1：平板电容器，两极板间距 $d$ 、带电量 $±Q$，中间充一层厚度为 $d_1$ 、介电常数为 $\varepsilon$ 的均匀介质。求电容。

解：将电容想象为两个电容串联，第一个电容是不夹电介质的电容器，第二个是填满电介质的电容器。

\[ C=\frac{1}{C_1}+\frac{1}{C_2}=\frac{d-d_1}{\varepsilon_0S}+\frac{d_1}{\varepsilon_0\varepsilon_rS}=\frac{\varepsilon_r(d-d_1)+d_1}{\varepsilon_0\varepsilon_rS} \]

得到

\[ C=\frac{\varepsilon \cdot S}{\varepsilon_r(d-d_1)+d_1} \]

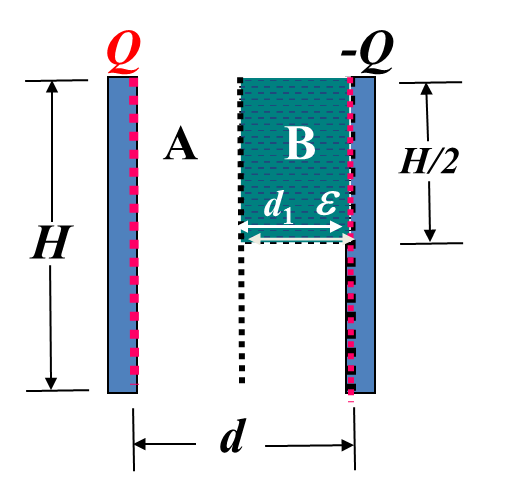
例题 2：平板电容器，两极板间距 $d$ 、带电量 $±Q$，中间充一层厚度为 $d_1$ 、介电常数为 $\varepsilon$ 但只占上半部分均匀介质。求电容。

将电容想象为两个电容并联，第一个电容又是两个电容串联（同例题 1 情况），第二个电容是不夹电介质的电容器。

\[ C=\frac{1}{\frac{1}{C_{11}}+\frac{1}{C_{12}}}+C_{2} \]

\[ C_{11}=\frac{d-d_1}{\varepsilon_0S};\,\,C_{12}=\frac{d_1}{\varepsilon_0\varepsilon_rS};\,\,C_2=\frac{d}{\varepsilon_0S} \]

连理即可。

静电场的能量 ¶

电容器的能量 ¶

\[ W=\frac{Q^2}{2C}=\frac{1}{2}CU^2=\frac{1}{2}QU \]

电场能量和电场能量密度 ¶

电场的能量密度为

\[ \omega_e=\frac{1}{2}\varepsilon E^2 \]

这说明介质在计划过程中也吸收储存了能量。

在各向同性的介质中可以写成

\[ \omega_e=\frac{1}{2}DE=\frac{1}{2}\overrightarrow D\cdot\overrightarrow E \]

恒定电场 ¶

恒定电流 ¶

常见的电流是在导线的两端加上电压后形成的。电流的大小用电流强度来描述。单位时间通过导体任一截面的电称作通过该截面的电流，用 $I$ 表示，即

\[ I=\frac{\mathrm{d}q}{\mathrm{d}t} \]

国际单位制中电流是基本物理量之一，单位为 $\mathrm{A}$ , $\mathrm{1A=1C\cdot s^{-1}}.$

电流并不能说明电荷通过截面上各点的情况，尤其对于大块导体，其不同部分的电流大小和方向都不一样。此外，对于高频交流电会有明显的趋肤效应，即使在细导线的横截面上也会形成一定的电流分布。为了描述导体中各处电荷定向运动的情况，需要引进电流密度 $\overrightarrow j$ 。

定义电流密度矢量：

\[ \overrightarrow J=nq\overrightarrow v \]

那么恒定电流，即为各处的电流密度不随时间发生变化。

\[ \int\kern{-8pt}\int \kern{-23mu} \bigcirc\, \overrightarrow J \cdot\mathrm{d}\,\overrightarrow s=0 \]

恒定电场 ¶

恒定的电荷分布产生不随时间改变的电场，这种电场称作恒定电场。对恒定电场，高斯定理显然是成立的，因为前面已有讨论，高斯定理是电磁场的普遍规律，它所根据的事实只是电场力的平方反比关系或电场线在无电荷处永不中断。而且，关于对称性较高的恒定电场，仍可用高斯定理方便地求出场强。

Info

恒定电场与静电场相似，都服从高斯定理和环路定理。它们的电荷分布都不随时间变化。

Info

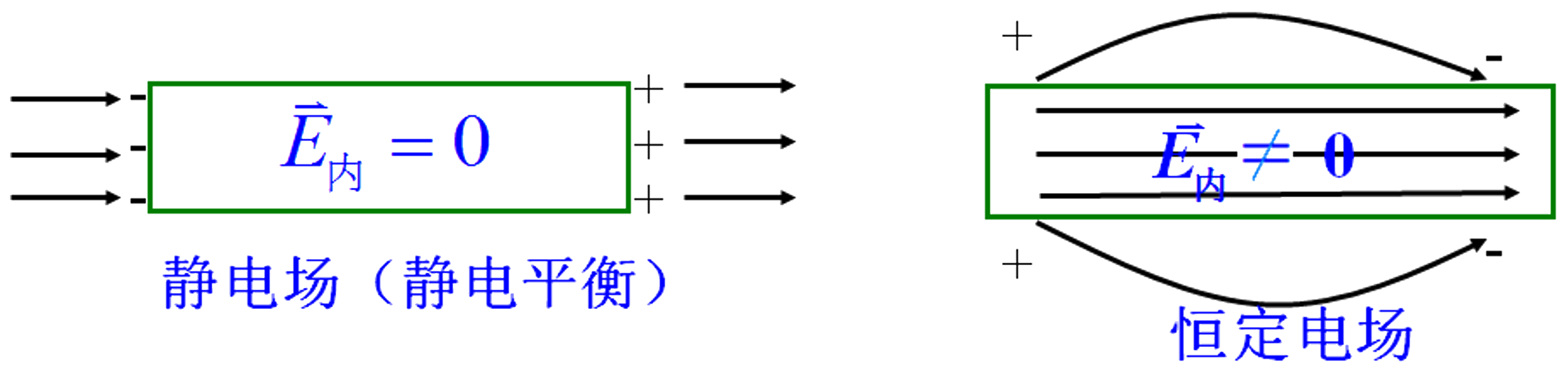
恒定电场与静电场的区别在于：

静电场导体内部场强为 0（无定向移动）；而恒定电场导体内部场强不为 0（有定向移动，电荷分布只是动态平衡）。
想要保持恒定电场，就要有外加电源来不断补充被损耗的电场能量。

非静电场和电动势 ¶

内容与高中基本一致。

需要注意的是电动势的方向是：电源内部由负极指向正极。

非静电场有时会布满整个电路。如温差电动势、感应电动势等。

欧姆定律的微分表达式：$\overrightarrow J=\sigma\overrightarrow E$ . 对于均匀材料，$\sigma$ 为常数。

均匀导体在恒定电场中，处处没有净电荷（只能在导体表面、两种导体的界面等）。

我去，相对论！¶

这里仅限于讨论匀速运动点电荷的电场，以及静止于场中的点电荷所受的作用力。

实验表明，高斯定理是经典电磁场的基本规律，即使在相对论效应明显的高速运动电荷的电场中同样成立。

电荷守恒定律总是成立的，即电荷的运动状态不改变其所带电荷的大小。这电荷的相对论不变性。

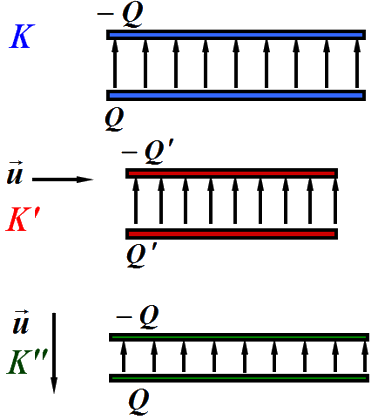
高速运动的平板电容器 ¶

对平板电容器做如下操作：

两个极板静止
两个极板沿着板子水平方向平移（速度垂直于场强方向）
两个极板垂直板子竖直方向平移（速度平行于场强方向）

考察板间场强的变化规律：

\[ \left\{ \begin{matrix} 1.\ \ \ \sigma_0=\frac{Q}{S}\ {\Rightarrow} \ E_0=\frac{Q}{\varepsilon_0 S} \hfill \\ 2.\ \ \ \sigma_\to=\frac{Q}{S\sqrt{1-\beta^2}}\ {\Rightarrow} \ E_\to=\frac{Q}{\varepsilon_0 S\sqrt{1-\beta^2}}>E \hfill \\ 3.\ \ \ \sigma_\downarrow=\frac{Q}{S}\ {\Rightarrow} \ E_\downarrow=E_0 \hfill \end{matrix} \right. \]

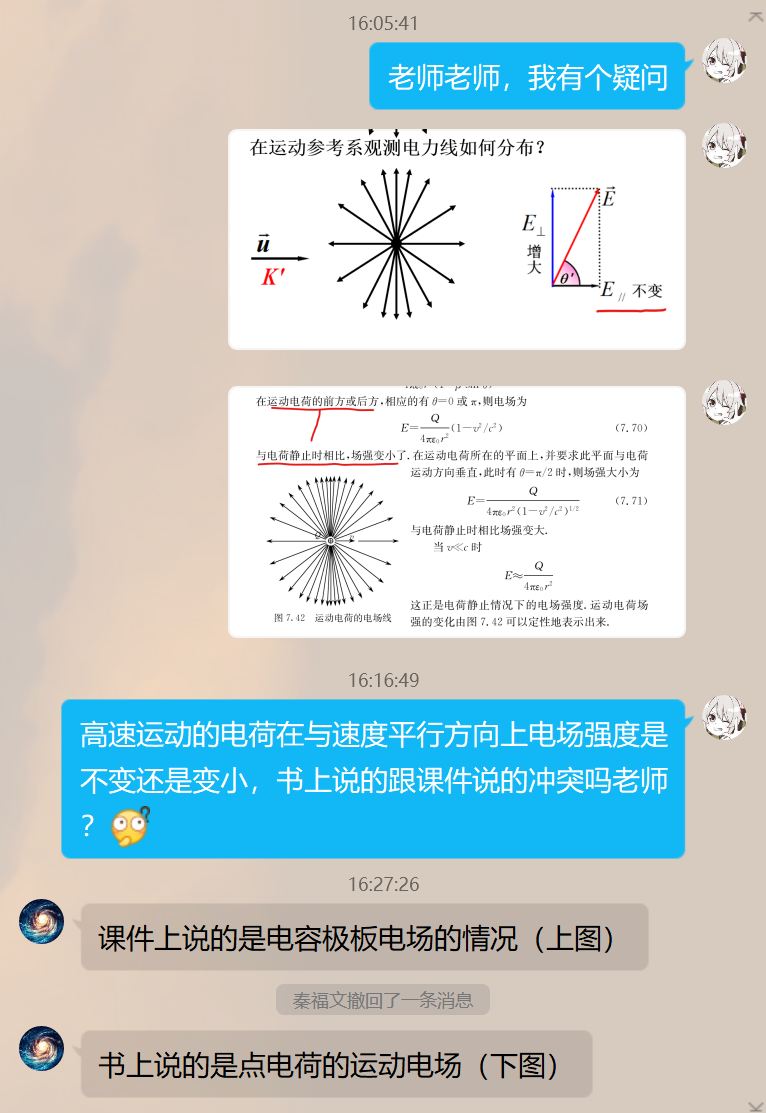
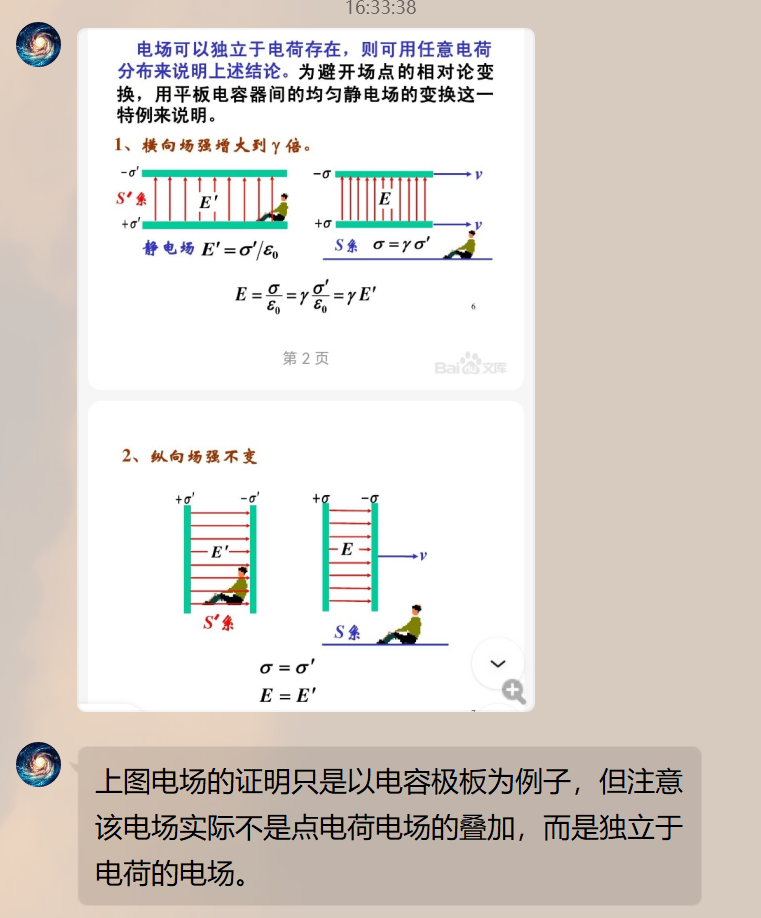
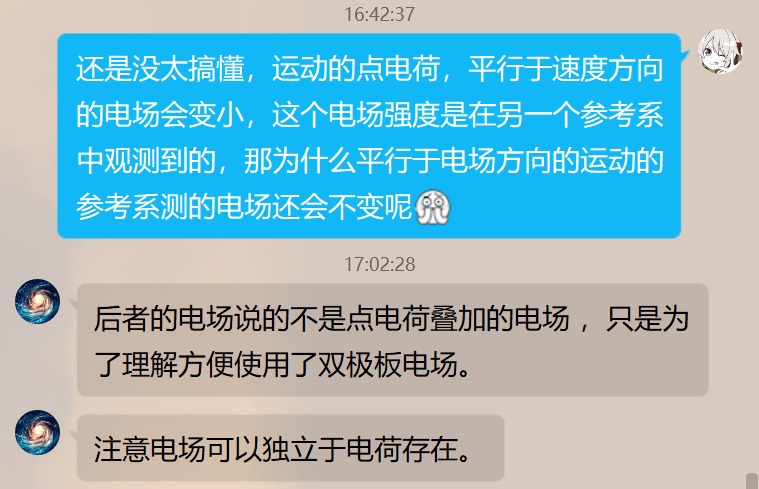
高速直线运动的电荷产生的场强 ¶

下面的所有公式不用记。但是要记住定性关系。

\[ \overrightarrow E=\frac{Q(1-\beta^2)}{4\pi\varepsilon_0 r^2(1-\beta^2\sin^2{\theta})^{3/2}}\frac{\overrightarrow r}{r} \]

这是一个高速直线运动电荷的空间场强分布公式，其中 $\overrightarrow r$ 表示点电荷到某点的指向。 $\beta=\frac{v}{c}$ 。 $\theta$ 是 $\overrightarrow r$ 指向与速度方向的夹角。

在运动电荷的前方或后方，相应的有 $\theta=0\,or\,\pi$ ，则电场为

\[ E=\frac{Q}{4\pi\varepsilon_0r^2}(1-\frac{v^2}{c^2}) \]

与电荷静止时对比，场强变小了。

在运动电荷垂直的方向，相应的有 $\theta=\pi/2$ 时，场强大小为

\[ E=\frac{Q}{4\pi\epsilon_0r^2\sqrt{1-\frac{v^2}{c^2}}} \]

与电荷静止时相比，场强变大了。

静电场 高斯定理

基本实验定律 ¶

电场强度及其叠加原理 ¶

场强 ¶

场强叠加原理 ¶

常见的电荷分布并求场强 ¶

点电荷 ( 系 ) ¶

电偶极子 ¶

细棒 ¶

均匀带电细圆环的轴线上 ¶

均匀带电薄圆盘的轴线上 ¶

高斯定理 ¶

电通量 ¶

高斯定理 ¶

场强环路定理 电势 ¶

电场力的功 ¶

场强环路定理 ¶

电势能 电势 ¶

电势能 ¶

电势 ¶

电偶极子的电势 ¶

场强与电势的关系 ¶

静电场中的导体 ¶

静电平衡状态和条件 ¶

导体的电荷分布 ¶

静电场中的电介质 ¶

电介质的极化 束缚电荷 ¶

电极化强度 ¶

电位移 电介质中静电场的高斯定理 ¶

电位移矢量 ¶

电容 电容器 ¶

电容 ¶

电容器 ¶

平板电容器 ¶

圆柱电容器 ¶

球形电容器 ¶

串联与并联 ¶

利用串并联巧解电容 ¶

静电场的能量 ¶

电容器的能量 ¶

电场能量和电场能量密度 ¶

恒定电场 ¶

恒定电流 ¶

恒定电场 ¶

非静电场和电动势 ¶

我去，相对论！¶

高速运动的平板电容器 ¶

高速直线运动的电荷产生的场强 ¶

评论

静电场高斯定理

场强环路定理电势 ¶

电势能电势 ¶

电介质的极化束缚电荷 ¶

电位移电介质中静电场的高斯定理 ¶

电容电容器 ¶