刚体的转动

约 1823 个字 2 张图片预计阅读时间 6 分钟

刚体的平动 ¶

任意质元运动都代表整体运动 . 根据前面质点系质心的定义和质心运动定理，可以完全确定刚体的运动规律 .

刚体的定轴转动 ¶

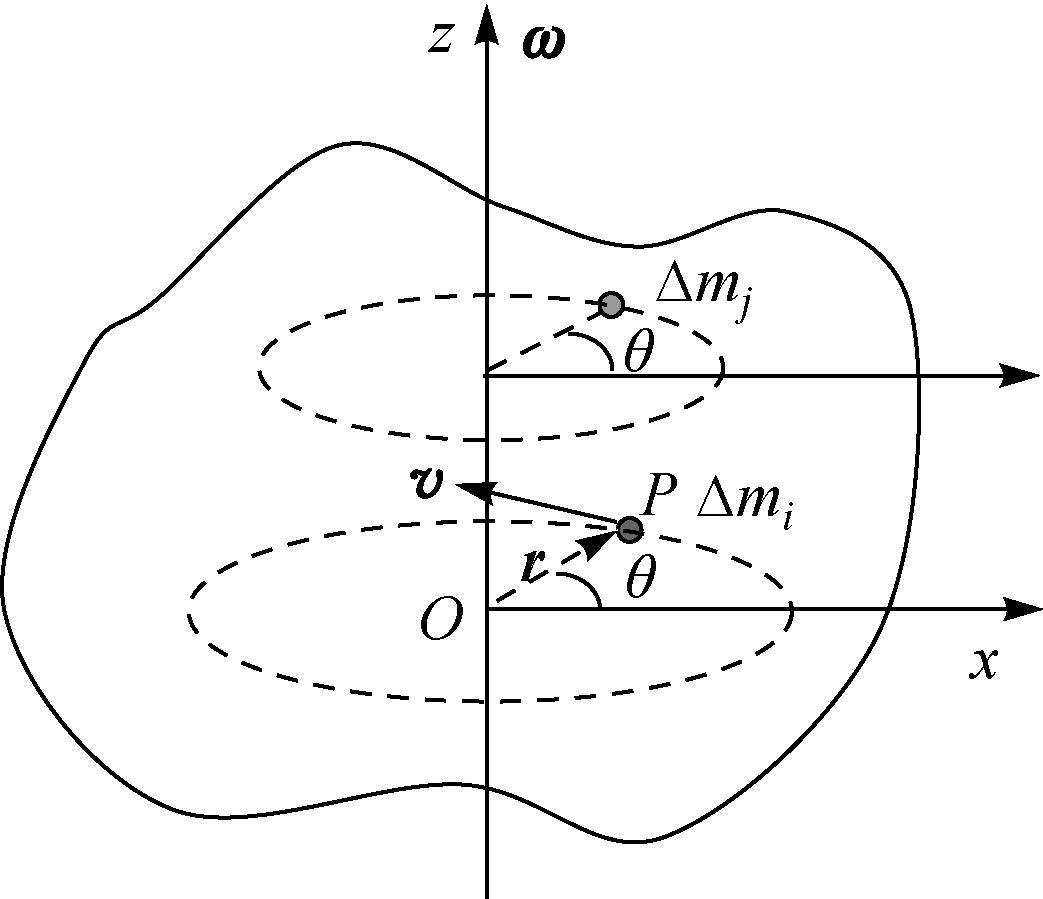
刚体运动过程中，如果其上有两个点不动，那么在两点连线上的各点也都不动，其他各点只能绕该直线做圆周运动 . 这条直线称为转轴，这样的运动称为刚体的定轴转动 . 如图 3.2 所示 .

由于各质点的相对位置保持不变，所有质点在相同的时间内转过相同的角度，故所有质点的角速度相同 .

用角量描述转动 ¶

角位移 $\Delta\theta$: ¶

在 $\Delta t$ 时间内刚体转动的角度 .

角速度 $\omega$: ¶

\[ \omega=\frac{{d}\theta }{{d}t} \]

$\omega$ 有方向，即 $\overrightarrow{\omega}$. 它的方向按右手螺旋法则确定 : 即当右手四指顺着转动方向，伸出的大拇指所指的方向就是的 $\overrightarrow{\omega}$ 方向 .

角加速度 $\alpha$: ¶

\[ \alpha=\frac{{d}\omega }{{d}t}=\frac{{d}^2\theta }{{d}t^2} \]

同样，$\alpha$ 也有方向，即 $\overrightarrow{\alpha}$. 它的方向与 $\overrightarrow{\omega}$ 相同 .

上述三个量称为角量 . 它们与位移 $x$，速度 $v$，加速度 $a$ 相互对应，这些称之为标量 . 下面探讨角量与线量之间的关系 .

角量与线量的关系 ¶

\[ S_{\text{路径}}=r\cdot{d}\theta \]

\[ v=\frac{{d}s}{dt}=r\frac{{d}\theta}{{d}t}=r\omega \]

\[ a_\tau=\frac{{d}v}{{d}t}=r\frac{{d}\omega}{{d}t}=r\alpha \]

\[ a_n=\frac{v^2}{r}=r\omega^2 \]

$a_\tau$ 是切向加速度，$a_n$ 是法向加速度 . （物理书 1.3 节）回忆: 曲率半径$\rho$，$a_n=\frac{v^2}{\rho}$.

刚体定轴转动定律 ¶

一些概念 : ¶

力矩 ¶

$P$ 为受力作用点，O 点为空间某固定点，$\overrightarrow{r}=\overrightarrow{OP}$，受力 $\overrightarrow{F}$，则定义力矩 $\overrightarrow{M}$:

\[ \overrightarrow{M}=\overrightarrow{r}\times \overrightarrow{F} \]

力矩的大小为 $M=rF\sin\alpha$，单位为 $N\cdot m$. 力矩的方向满足右手螺旋定则.

动量矩（角动量）¶

$P$ 为某质点，其质量为 $m$，速度为 $\overrightarrow{v}$，动量为 $\overrightarrow{p}=m\cdot\overrightarrow{v}$. O 点为空间某固定点，$\overrightarrow{r}=\overrightarrow{OP}$，则定义动量矩（亦称角动量）$\overrightarrow{L}$:

\[ \overrightarrow{L}=\overrightarrow{r}\times \overrightarrow{p}=\overrightarrow{r}\times (m\overrightarrow{v}) \]

角动量的大小为 $L=rp\sin\theta=rmv\sin\theta$，单位为 $kg\cdot m^2\cdot s^{-1}$. 角动量的方向满足右手螺旋定则.

** 注意 : 力矩和角动量都是对同一固定点的 . **

回忆 : 角动量定理和角动量守恒定律（物理书 2.4 节）¶

质点系的角动量定理 ¶

由于内力总是成对出现，所以系统内所有内力的矩的矢量和为零 .
质点系的角动量定理即一个质点系所受的合外力矩等于质点系角动量的时间变化率 .
所谓质点系的角动量就是系统内所有质点的角动量的矢量和 .
系统受外力矩作用，系统角动量就会发生变化，内力矩会改变系统内单个质点的角动量，但不会影响系统的总角动量 .

用公式表述即为 :

\[ \overrightarrow{M}_\text{外}=\frac{{d}\overrightarrow{L}}{{d}t} \]

角动量守恒定律 ¶

当质点系所受合外力矩为 0 时（$\overrightarrow{M}_\text{外}=0$），质点系的总角动量保持不变（$\sum{\overrightarrow{L_i}}=const$）

刚体定轴转动定律 ¶

转动惯量 ¶

对于转轴确定的刚体，$\sum_{i}m_ir_{r}^2$ 是一个常量，称为为刚体对该轴的转动惯量，用 $J$ 表示，即

\[ J=\sum_{i}m_ir_{r}^2 \]

$J$ 是一个刚体和一个轴的固有属性 . 它的 SI 单位制是 $kg\cdot m^2$

定律 ¶

刚体对轴的角动量 $\overrightarrow{L_z}$ 可以表示为 :

\[ \overrightarrow{L_z}=J\cdot\overrightarrow{w} \]

而由角动量定理（$\overrightarrow{M}_\text{外}=\frac{{d}\overrightarrow{L}}{{d}t}$）代入得 :

\[ \overrightarrow{M}_\text{z}=\frac{{d}(J\overrightarrow{w})}{{d}t}=J\overrightarrow{\alpha} \]

可见，在外力矩作用下，刚体绕轴做加速转动 . 角加速度与轴向外力矩成正比，与转动惯量成反比 . 这就是刚体的定轴转动定律，它是解决刚体定轴转动动力学问题的基本方程 . 根据该定律，在相同外力矩作用下，转动惯量大的刚体，其角加速度小，即角速度变化慢，说明其转动状态不易发生改变 . 这样的刚体，我们常说其转动惯性大，转动惯量就是刚体转动惯性的量度 . 从前面的分析、推导过程可知，刚体的定轴转动定律，实际上就是质点系角动量定理应用于刚体绕定轴转动时的特殊表现形式.

刚体的转动惯量与三个因素有关，转轴的位置、刚体的质量及质量对轴的分布情况 . 形状、大小相同、质量均匀分布的刚体，总质量越大，转动惯量越大 ; 总质量相同的刚体，质量分布离轴越远，转动惯量越大 ; 同一刚体，对应不同的轴，转动惯量不同 .

对于角动量守恒定律，可重写为刚体定轴转动的角动量守恒定律:

\[ M_z=0 \text{ 时，}\overrightarrow{L_z}=J\overrightarrow{\omega}=const \]

计算转动惯量 ¶

叠加定理 转动惯量是标量，由几个物体组成的刚体的转动惯量等于各个物体相对于同一转轴转动惯量之和，即

\[ J=\sum_{i}J_i \]

平行轴定理质量为$m$的刚体，对于通过其质心$C$的轴的转动惯量为$J_C$，若另一轴与过质心的轴平行且相距为$d$则刚体对该轴的转动惯量为

\[ J=J_C+md^2 \]

垂直轴定理或正交轴定理薄板状刚体对板内两正交的 $x$ 轴和 $y$ 轴的转动惯量之和等于该刚体对通过两轴交点垂直于板面的 $z$ 轴的转动惯量，即

$$ J_z=J_x+J_y $$

常用转动惯量 ¶

刚体转动的动能定理 ¶

外力矩的功 ¶

力 $\overrightarrow{F}$ 对刚体做的功可表示为 :

\[ A=\overrightarrow{F}\cdot \overrightarrow{r}=\overrightarrow{M}\cdot{\Delta \theta} \]